You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Help, properties of a curve/circle
- Thread starter Noel
- Start date

Help Support UKworkshop.co.uk:
This site may earn a commission from merchant affiliate
links, including eBay, Amazon, and others.
novocaine
Established Member
doctor Bob
Established Member
- Joined
- 22 Jun 2011
- Messages
- 5,171
- Reaction score
- 1,881
Do you know the height of the segment?
If you do there is a formula.
If you do there is a formula.
Eric The Viking
Established Member
- Joined
- 19 Jan 2010
- Messages
- 6,599
- Reaction score
- 76

Pythagoras's Theorem, sines and cosines will get you there.
The black line is your string. The red line you haven't told us yet, but you need to measure it.
Crucially, the shape of the triangles A and B is the same, but the sizes are different. This is because wherever a triangle from the diameter of a circle touches its edge, the angle is always 90 deg. (the triangle made by the green and blue lines). The big triangle is also the same shape, as it shares the same angles with the other two.
So work out the missing distance in triangle A (the green line of it). That can be dropped into the big triangle, allowing you to work out both the other green line and eventually getting you to the diameter of the circle (blue).
Note that this is an approximation, because the "bowstring" method actually makes a bit of a parabola or a catenary (a proper engineer will be along in a minute...), NOT an arc of a circle. But it's probably close enough for your needs.
You need a calculator that can do sines, cosines and arcsines, etc. as you'll be swapping between angles and distances. It also probably needs to do degrees (at least I find them easier than radians!).
HTH, E.
Attachments
doctor Bob
Established Member
- Joined
- 22 Jun 2011
- Messages
- 5,171
- Reaction score
- 1,881
If you know A above, then it's a simple formula with no sins, cosines etc.

£238.91
£360.17
Trend Portable Benchtop Router Table with Robust Construction for Workshop & Site Use, 240V, CRT/MK3
Amazon.co.uk

£24.99
Facemoon Reusable Masks,Safety Masks,Dual Filter Masks, Paint, Dust, Epoxy Resin, Construction, Welding, Sanding, Woodworking, Chemical Reusable Gas Masks
ShenZHEN CIRY MINGYANG LITIAN ELECTRONIC ECOMMERCE

£12.50 (£1,250.00 / kg)
£14.45 (£1,445.00 / kg)
JSP M632 FFP3moulded Disposable Dustmask (Box of 10) One Size suitable for Construction, DIY, Industrial, Sanding, dust protection 99 Percent particle filtration Conforms and Complies to EN 149
Amazon.co.uk

£17.99 (£1.80 / count)
£27.44 (£2.74 / count)
3M 8822 Disposable-fine dust mask FFP2 (10-pack)
Amazon.co.uk

£19.99
Respirator Mask,Safety Dust Face Cover,Dust Face Cover Paint Face Cover,Gas Mask With Filter,For Paint,Dust And Formaldehyde,Sanding,Polishing,Spraying And Other Work
ShenZHEN CIRY MINGYANG LITIAN ELECTRONIC ECOMMERCE

£16.59
£25.00
Woodworking Joinery by Hand: Innovative Techniques Using Japanese Saws and Jigs
Amazon.co.uk
Yojevol
Clocking on
This is a difficult problem to solve with the info given, but not impossible if you have the relevant mathematical software available. Fortunately it is available at https://planetcalc.com/1421/
This screenshot gives the answers with your data fed in:-

Brian
This screenshot gives the answers with your data fed in:-

Brian
Attachments
Sheffield Tony
Ghost of the disenchanted
I'm fairly sure a rod tensioned by a string will not be a circular arc.
gasman
Established Member
No it will be a parabola which doesn't have a radius. It wont be too far away from an arc if it is 'shallow' though so the formulae above will be a reasonable approximation
cheers mark
cheers mark
MikeG.
Established Member
Noel":2qtbtcls said:Is there a way of finding out the radius or any other properties of a circle with only the following information:
(very technical drawing of flexible rod pulled into a curve with string)
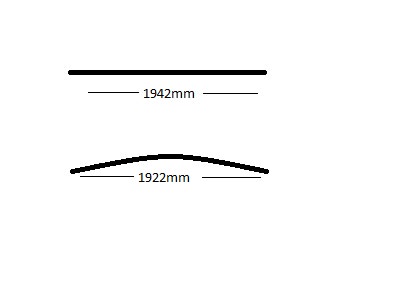
7816mm diameter
As an aside, the distance "A" from ErictheViking's diagram is approx 120mm.
Tasky
Established Member
No, it won't.Sheffield Tony":17ds50pm said:I'm fairly sure a rod tensioned by a string will not be a circular arc.
More importantly, people have been hand-making bloody good and accurately sized Longbows for centuries, without having a clue who Pythagoras even was... So there must be some even simpler tricks!!
Eric The Viking
Established Member
- Joined
- 19 Jan 2010
- Messages
- 6,599
- Reaction score
- 76
doctor Bob":10gnc4ut said:If you know A above, then it's a simple formula with no sins, cosines etc.
Quite right - just pythagoras as they are all right-angled triangles. I was being a twit... ;-)
Johnboy
Established Member
Using CAD to draw it the radius is 3900. The rise is 120.254.
John
John
handymath.com/cgi-bin/arc18.cgi
This site calculates several parameters. Radius 3900mm with the assumption that the shape is an arc.
This site calculates several parameters. Radius 3900mm with the assumption that the shape is an arc.
Similar threads
- Replies
- 40
- Views
- 2K
- Replies
- 50
- Views
- 3K




























