Shelving Spacing Problem

[woodyone]

After many attempts of trying to figure this out i give up.. This is for a job of a tall bookcase 2700 high. i am trying to figure out an consistent spacing for the shelves from a large space at the bottom to a small space at the bottom.

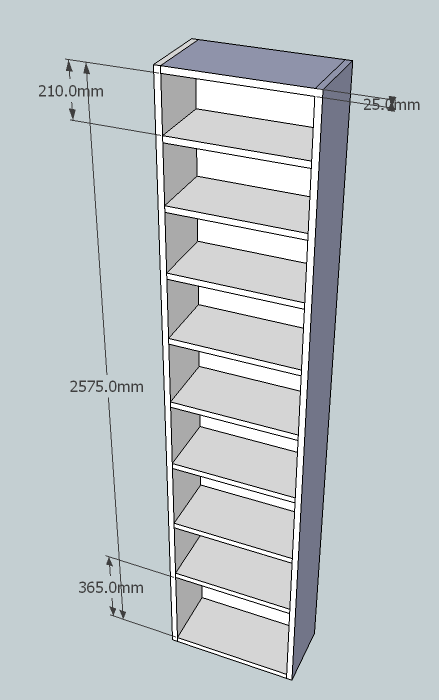
Right the problem. i know my measurement for the top shelf ( 210 mm ) and i know my measurement for my bottom shelf ( 365 mm ) i also know how many shelves ( 9 ) and i know how much space i have for the shelves ( 2575 mm) but if you exclude the thickness of materials for you are left with ( 2375 mm ).

i want the shelves to consistently reduce in size from 365 mm to 210 mm over 9 shelf spaces with them all adding up to 2375 mm.

Here is a picture if i haven't explained my self clearly.

Many Thanks,

Woody.

 

[WoodMangler]

According to my rather rusty maths, it can't be done: 210 to 365 in nine consistent steps only adds-up 2241. You need to enlarge the first and/or last gaps to make it work - 227 to 382 comes pretty close at 2377.88, for instance.

eta: your 210-365 in 2375 would be very close if you upped the number of shelf-gaps to 11 :-

210
226
241
257
272
288
303
319
334
350
365
---
2379 - so reduce 4 of the gaps by 1mm

 

[WellsWood]

Hi Woody, yes understand your problem exactly, always a headscratcher this one.

Try THIS - the first three give different ways of calculating progressively smaller spaces. They're meant for drawers but will work equally well with your problem.

edit
just tried it and can't get the arithmetic one to work, but using geometric progression (second calc in list) and using a common ratio (multiplier) of 1.0822 works and gives the following heights (drawers = gaps between shelves):

Drawer Height (cm)
1 21.00
2 22.73
3 24.59
4 26.62
5 28.80
6 31.17
7 33.73
8 36.51

 

[Sheffield Tony]

I agree t is not possible with a linear graduation - but I get the other way around - the height would be 2587.5 + the thickness of the materials. There are too many shelves; you would need a taller cabinet, fewer shelves or smaller at one end, or both. Or a non-linear graduation, like this (0 is top shelf, 8 is bottom)

0 210
1 212
2 218
3 228
4 247
5 269
6 296
7 328
8 365

This is shelf i = 210 + k1 * i + k2 * i * i where k1 = -0.99 and k2 = 2.54. Rounding to the nearest mm means the above numbers add up 2 mm short of 2375, but it is close. Whether it looks good, I dunno. Perhaps there are other established ways of doing this ?

 

[siggy_7]

Your first shelf height is 210mm, your 9th shelf height is 365mm, you want even spacing between them. Therefore shelf 9 has a height of 210mm plus 8 times your gap increment. 210 + 8x = 365, therefore x is 19.375mm. So each shelf spacing needs to be 19.375mm greater than the last, given your dimensions. This is the only solution to your problem of spacing the shelves evenly, but as others have said it won't give you the specified height of the cabinet - which is why you're struggling!

 

[WoodMangler]

Your first shelf height is 210mm, your 9th shelf height is 365mm, you want even spacing between them. Therefore shelf 9 has a height of 210mm plus 8 times your gap increment. 210 + 8x = 365, therefore x is 19.375mm. So each shelf spacing needs to be 19.375mm greater than the last, given your dimensions.

But that doesn't give the required total height of 2375.

 

[siggy_7]

But that doesn't give the required total height of 2375.

Edited my post when I realised that, but you beat me to it.

 

[marcros]

i know that it isnt the question that you are asking, but would shelves that increase in height by 15 or 20mm per shelf actually be that useful? The books that I have seem to be a similar height for novels and the remainder fit into either medium or large. If I were making this for myself, for my home, I would want a number of small shelves, a number of medium and a number of large. Otherwide my novels would look increasingly lost on the mid shelves and the unit wouldnt look quite right.

just my thoughts though...

 

[AndyT]

I think Marcros is right - you're asking the wrong question!

 

[Racers]

Hi, Woody

I did a shelving unit with graduated shelves like that and ran into problems fitting books in.
As Marcros said some big some medium some small.

Pete

 

[Chrispy]

Make the shelves adjustable and let the client work it out. :wink:

 

[woodyone]

Thanks everyone for the input, this is exactly what i'm after, wellswood calculator seem very handy and i have bookmarked. but what tony has said is what i have been trying to achieve and i have just put it into sketch up and it looks good.

i want to do this mostly for effect as the bookcase is so tall i think that it will work well in perceptive, as for the spacing of the shelves i feel the same about have books to fill the staggering sizes in shelves but. there will be about six of these bookcase in the room , and i quote " i will find books to fill it". i am still and design and quote stage in this job and will have other layout of the shelves to show the client if she doesn't like the staggered look.

Thanks!

 

[WellsWood]

Yep those woodcalcs are indispensable, you may want to check the edit to my post for an alternative layout.

On balance though I'm firmly in Chrispy's camp of making them adjustable. Impress on the client how much they'll thank you for it in a couple of years when they change their mind about what they want to put on the shelves.

 

[Phil Pascoe]

I don't know how to post a drawing, but my old oak bookcase has adjustable shelves - it has two full height inserts opposing each other in each end that are cut like the teeth of a rip saw, and a piece of wood about the section of heavy doorstop fits between opposite pairs of teeth (the teeth would be maybe 35mm-40mm high). The shelves are then notched front and back to go around the uprights and sit on the cross pieces.
You could make a templet for marking out, you'd have to cut them out of course,but it's quite a cheap option when you consider the cost of inserts, brackets and commercial systems. It's old fashioned, but it works.
Phil.

 

[woodyone]

i do agree that its easier to make them adjustable but i don't think the client felt too strongly about either holes of strips in the side of the bookcase. also there will be four of these bays next to each other and i think the client likes the idea of every thing lining up. also the design is based on a fitted bookcase in a bookshop which has these quite chunky fixed (25mm) shelves, which also stagger in size.

 

[Sheffield Tony]

Just to correct myself - the 2 mm short isn't because of rounding, it's because I made a slip - shelf 3 in my list above should be 230, not 228. Then it adds up nicely.

 

[woodyone]

Ok Thanks for your help, i dont really understand your equation but obviously it works. would that sort of equation be able to be put into a spreadsheet so that you just plug in numbers?

 

[AndyT]

I don't know how to post a drawing, but my old oak bookcase has adjustable shelves - it has two full height inserts opposing each other in each end that are cut like the teeth of a rip saw, and a piece of wood about the section of heavy doorstop fits between opposite pairs of teeth (the teeth would be maybe 35mm-40mm high). The shelves are then notched front and back to go around the uprights and sit on the cross pieces.
You could make a templet for marking out, you'd have to cut them out of course,but it's quite a cheap option when you consider the cost of inserts, brackets and commercial systems. It's old fashioned, but it works.
Phil.

I've built one like that to fill an alcove in our sitting room - I liked the triple whammy of it being traditional, adjustable and cheap!

That said, I've never changed the positions of the shelves from the day I put it up...

 

[Shed boy]

It is possible to space these evenly, as follows
The height from floor to underside of 1st shelf = (365 +25) ie 390
The height from the under side of top shelf to underside of the top = (210+25) ie 235
You have to loose 390-235mm over 8 shelves
ie 155/8 - 19.375 mm
So the spacing from underside to underside of each subsequent shelf is as follows
390
370.625
351.250
331.875
312.50
293.125
273.750
254.375
235.00

obviously a bit of rounding off is required

cheers

euan

 

[Sheffield Tony]

But these numbers add up to 2812.5 mm total height.

You cannot solve this problem (exactly at least) by an arithmetic progression (each height is larger than the previous by a constant increment) or geometric progression (each height is larger than the previous by a fixed multiplier), because in either case you have only one variable to select (the increment, or multiplier) but you must meet two constraints. One is due to the graduation, the other is the overall height.

That's why in my example, I used a quadratic equation for the shelf spacings - same number of parameters to select as there are constraints.

In case anyone is interested, this is my working.

Let the nine spacings be x0, x1, ... x8

where the i'th spacing is

xi = a + b*i + c*i*i

the top shelf, i=0, is 210 wide, so

210 = a

The bottom shelf, i=8, is 365 :

365 = 210 + 8*b + 64*c
I.e. 8*b + 64*c = 155 (1)
The overall height (minus 8 25 mm thick boards) need be 2375. This is the fun bit. You need to know that the sum of the integers from 1 .. n is 1/2*n*(n+1), and the sum of their squares is 1/6*n*(n+1)*(2*n+1), which for n=8 are 36 and 204 respectively. So:

Total of spacings = 2375 = 9*a + b*36 + c*204
or 36*b + 204*c = 485 (2)

Multiplying (1) by 4.5 and subtracting (2) gives
84*c = 213.5
c = 2.54166
Substitute in (1) to get b=-0.98833

So, for those teachers at school who dismissed woodwork as being not a very academic subject ...